Неупругий удар (задача)

[warstuser]

Да вот сколько бы не смотрел задачи про баллистические маятники ( пуля --> песок), везде пользуются законом сохранения энергии. Только вот не пойму в чем логика не верна.

[DimaM]

warstuser в сообщении #688249 писал(а):

Да вот сколько бы не смотрел задачи про баллистические маятники ( пуля --> песок), везде пользуются законом сохранения энергии.

А нельзя ли пример? Только не своими словами, а точную цитату.

[gris]

Я бы посоветовал ТС решить эту задачу в общем виде и оценить зависимость относительной разницы ответов от соотношеня масс.
Ну ладно, давайте посмотим, а то вдруг и вправду энергия сохраняется .
В висящий мешок массой $M$ влетает пуля массой $m$ со скоростью $v$ и застревает. Чего там дальше происходит? Рассмотрим задачу в системе отсчёта, связанной с неподвижной опорой. По закону сохранения импульса $mv=(M+m)u$, где $u$ — скорость мешка с пулей сразу после удара.
Отсюда получаем $u=\dfrac {mv}{M+m}$. Кинетическая энергия конструкции

$2K=(M+m)u^2=\dfrac {m^2v^2}{M+m}=mv^2\cdot \dfrac {m}{M+m}$.

То есть прежняя кинетическая энергия умножается на множитель $\dfrac {m}{M+m}$. Поскольку это выражение для положительных масс всегда меньше единицы, то получается, что при абсолютно неупругом ударе кинетическая энергия всегда уменьшается. И уменьшается в $\dfrac {M+m}{m}=1+\dfrac Mm$ раз. То есть, если масса пули равна массе мешка, то "передастся" (в Вашей терминологии) ровно половина кинетической энергии. Если масса пули очень мала по сравнению с массой мешка, то почти вся энергия перейдёт в тепло и прочие трудные для измерения виды.

Максимальная высота подъёма прямо пропорциональна кинетической энергии после удара, поэтому относительная ошибка будет такая же. Но так как обычно баллистический маятник используется для вычисления скорости пули по максимальной высоте подъёма(углу отклонения), то там появляется корень квадратный и относительная ошибка в определении скорости может составить $\sqrt {\dfrac {M+m}{m}}$ раз в сторону занижения.
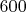
Например, если масса мешка $9$ кг, а масса пули $9$ г, то вы рискуете получить скорость $20$ м/с вместо правильной $600$ м/с.

* Под относительной ошибкой я понимаю максимальное из двух отношений верного и ошибочного значения. То есть абсолютная погрешность в логарифмической шкале.

[warstuser]

Убедили))