Предел

[arqady]

Найдите $\lim e^{-\frac{ n}{2}}\sqrt n\sqrt[n]{\binom{n}{0}\binom{n}{1}\cdot...\cdot\binom{n}{n}}$

[Руст]

Это равно

$$\lim_{n\to \infty}exp(-\frac{n}{2}+\frac{1}{2}\ln n +\frac{1}{n}[(n-1)\ln (n!)-2\sum_{k=1}^{n-1}\ln(k!)]).$$

Вычисляем $\ln(k!)=\frac{1}{2}\ln(2\pi )+(k+\frac 12)\ln k -k+\theta_k, |\theta_k|<\frac{1}{2k}$.
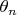
Ясно, что все $\theta_k$ и $\theta_n$ можно выбросить без ущерба для вычисления предела.
Тогда под экспонентой остаются

$$-\frac{n}{2}-\frac{n-1}{2n}\ln{2\pi}+\ln n(\frac{1}{2}+\frac{(n-1)(n+\frac 12)}{n})-(n-1)+(n-1)-\frac{2}{n}\sum_{k=1}^{n-1}(k+\frac 12)\ln k.$$

Последнюю сумму можно оценить интегрированием от 3/2 до n-1/2, так как вторая производная $\frac 1x$ мала и ошибка после деления на $n$ устремится к 0.
Это дает $n\ln(n-\frac 12)-\frac{n-1}{2}+o(1)$ для этой суммы (с умножением на 2/n). В итоге под экспонентой получаем
$-\frac 12 \ln(2\pi)+n(\ln n-\ln(n-\frac 12))-1/2+o(1)=\frac{1}{2}\ln(2\pi)+0(1)$.
Значит предел равен $\frac{1}{\sqrt{2\pi}}.$