Почему ноль? То, что написал Someone - это Alt B(x,y). Если B - симметрическая форма, то есть

, то да, в скобках будет ноль, но такое же не всегда верно.
Вот вам пример несимметрической билинейной формы:

,

Делаем из нее две формы:

и
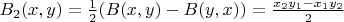
Теперь

- симметрическая,

- кососимметрическая, и в сумме они дают В. То есть, мы разложили В на симметрическую и кососимметрическую компоненты.