Да, попробовал эту формулу для тех значений, что у Пиросона (50,75,100,150) - где-то близко. Еще попробовал формулы для

(уравнения 20-23). Если я правильно понял эти уравнения, то там нужно по выборкам объема

считать

, потом по получившейся выборке

-статистик считать

и

, правда там в уравнениях присутствует величина

, которую я в этих уравнениях не понимаю, ведь зависимость

и

задается уравнением 12. Так вот, более менее похоже получается только для среднего и для

, а для

и
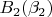
мало похоже.
Вопрос такой - а можно ли увеличить точность оценки распределения при малых

увеличив ряд разложения? Учитывать не только слагаемые порядка

, но и дальше, предположим до

.