"При изоморфном соответствии между группами

и

единице группы
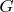
соответствует единица группы

, и если элементу

из

соответствует элемент

из

, то элементу

соответствует элемент

" (Курс высшей алгебры. Курош 14 глава). В учебнике это не доказывается.
Первое я попытался доказать так:

,

,

,

,

,

,

, значит

,

,

,

. Где-то ошибся? (меня смущает, что у меня получилось равенство, а не соответствие).
Второе- так:

,

,

,

. Перемножаем равенства и получаем в силу


, отсюда

.
Думаю, что ошибка есть (см. замечание к первому пункту).
Как научиться доказывать изоморфность, а не равенство?