и еще один диффур:

[laptop]

дан диффур $x'+2x-\frac{1}{1+t^{5}}x^{2}=0$
задача: выписать все решения, определенные при $t\ge0$ и стремящиеся к нулю на бесконечности

значит общее решение$c e^{2t}$
решение хотелось бы найти, но интеграл не берется
решение запишется:
$y=(-\int \frac{e^{-2t}}{1+t^{5}}dt+c_{1})e^{2t}$
ну и понятно, что раз нужно, чтобы стремилось к нулю, занулим $c_{1}$
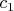
так вот. остается оценить оставшуюя штуковину, что как-то не очень выходит. могу в качестве верхней оценки получить 0.5. меньше никак не выходит..

[ИСН]

laptop в сообщении #677167 писал(а):

значит общее решение$c e^{2t}$

вот это место поподробнее

[laptop]

да уж. кажется от сессии ум за разум заходит. спасибо)