добрый день
необходимо найти площадь боковой поверхности следующего конуса: основание - окружность радиуса

, вершина конуса удалена на расстояние

от основания и на высоте

над плоскостью основания:
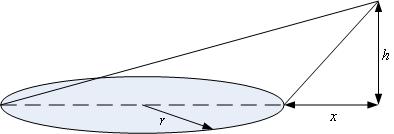
Т.е. образующая не является константой. Если разрезать этот конус по наименьшей образующей

, развернуть и затем "положить" его одной из сторон разреза на ось

, то получим приблизительно следующую картину:
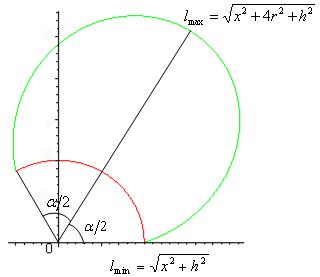
красной линией показан разрез прямого кругового конуса с радиусом основания

. Площадь боковой поверхности будет площадь фигуры, ограниченной зеленой линией и осью координат. Возникает вопрос, как посчитать эту площадь, т.к. интегрировать напрямую нельзя, т.к. функция неоднозначна.
У меня были следующие мысли по поводу зависимости длины образующей

от угла развертки

: т.к. при

и при

образующая минимальна и равна

, а при

- максимальна

, то ее вид

. Если это правильно, то можно попробовать повернуть развертку на угол

(т.е. чтобы наибольшая образующая совпала с осью

) и разбить полученную фигуру на несколько частей, каждая из которых будет либо ограничена однозначной функцией, либо какими либо прямыми. Что скажете?