Здравствуйте!
В процессе работы возникло следующее уравнение на неизвестную величину

:

где

и

- имеют очень громоздкую зависимость от

, настолько громоздкую, что вычислять их можно только на компьютере. Известо лишь, что числа эти положительные и очень быстро убывают при больших

(по-видимому как

). Однако первые шесть величин

и

возрастают.

- известное число.
Решение должно удовлетворять неравенству
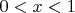
.
Есть ли способы решения таких задач? Возможно, это уравнение можно свести к интегральному?
Можно ли переформулировать задачу так, что она будет пригодна для решения на ЭВМ? Особый интерес представляет случай

при всех

. Заранее спасибо!