Всем привет!
Направьте, пожалуйста, в сторону решения такой задачи. Есть линейный функционал
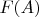
, норму которого надо оценить через норму

, причем

:

.
Сначала я выписал несколько первых членов этой суммы (посмотреть, что имеется):

.
По логике:

.
Что дальше делать - не совсем понятно. Или я вообще неправильно действую - и можно по-другому?
Спасибо.