Класс всех моделей Г

[gefest_md]

Объясните, пожалуйста, почему если множество предложений первого порядка $\Gamma$ имеет бесконечную модель, то множество (класс) всех моделей $\Gamma$, $Mod(\Gamma)$, строго больше чем любое множество $X$?

Вот цитата из учебника:

Цитата:

... $Mod(\Gamma)$ is sometimes unbounded. It is unbounded precisely when $\Gamma$ has an infinite model. By unbounded we mean that for any set $X$, $Mod(\Gamma)$ is strictly bigger than $X.$ ...

[Aritaborian]

Боюсь, вы неверно перевели. Там одно не следует из другого, это просто идущие подряд определения.

[gefest_md]

Aritaborian в сообщении #662360 писал(а):

... определения.

Так как это два определения, то по идее они равносильны. Мне кажется надо это доказать. Нет

[Aritaborian]

Ну смотрите. Имеем:

Цитата:

... $Mod(\Gamma)$ иногда неограничен. Он ограничен в точности, когда $\Gamma$ имеет бесконечную модель. Говоря «не ограничен» мы имеем в виду, что для любого множества $X$, $Mod(\Gamma)$ строго больше, чем $X.$ ...

Не вижу, что тут нужно доказывать.

(Оффтоп)

В самом предмете не разбираюсь, просто пытаюсь рассуждать логически.

[gefest_md]

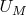
Подумав лучше, придумал такое решение. Пусть дана модель множества предложений $\Gamma$: $M=(U_M|\nu)$, где $U_M$ - универсум, а $\nu$ - сигнатура. Пусть также $X$ - произвольное множество. Тогда моделями $\Gamma$ будут также структуры:

$M_1=(U_M|\nu_1)$

$M_2=(U_M|\nu_2)$

$M_3=(U_M|\nu_3)$

$\dots$

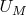
где $\nu_i$ получается добавлением в $\nu$, в качестве константы, какого-нибудь элемента из $\mathcal{P}(X)$. Тогда $|Mod(\Gamma)|\geqslant|\mathcal{P}(X)|>|X|$, что и требуется. Но замечаю, что $U_M$ не обязана быть бесконечной.

[gefest_md]

Всё верно. Модель должна быть бесконечной, если рассматривать произвольное, конечное $X$.

Уже не понимаю, как может допускаться такое определение неограниченного множества? Разве $Mod(\Gamma)$ может быть строго больше любого множества $X$? $|Mod(\Gamma)|<|\mathcal{P}(Mod(\Gamma))|$.