Помогите разобраться с задачей на цепи Маркова

[Polly_Molly]

Пусть $\xi_0, \xi_1$ ... - цепь Маркова с множеством состояний {1,2,3}, матрицей переходных вероятностей ($p_{ij}$) и стационарным распределением $\pi_j$. Показать, что если $p_{11}=p_{22}=p_{33}=0$ и $\pi_1=\pi_2=\pi_3=1/3$, то $p_{12}=p_{23}=p_{31}$ и $p_{13}=p_{21}=p_{32}$.

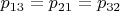
Я воспользовалась формулами $\sum_{j=0}^{\infty} \pi_j=1$ и $\pi_j=\sum_{i=0}^{\infty} p_{ij}\pi_i$

Получилась система:

$$ \left\{ \begin{array}{rcll} \pi_1+\pi_2+\pi_3=1\\ p_{21}\pi+p_{31}\pi}=1/3\\ p_{12}\pi+p_{32}\pi=1/3\\ p_{13}\pi+p_{23}\pi=1/3\\ \end{array} \right $$

Преподаватель сказала, что вроде как правильно решаю, и осталось выразить отсюда,что вероятности равны. Но я совсем не понимаю, как из такой системы это можно показать. Может не хватает каких-то формул или данных?.. Пожалуйста, помогите разобраться!

[--mS--]

Что за $\pi$ в уравнениях? Ещё стоит вспомнить, что матрица вероятностей перехода - стохастическая, т.е. сумма вероятностей в каждой строке равна единице.

[Polly_Molly]

$\pi$ из формулы $\pi_j=\sum_{i=0}^{\infty}p_{ij}\pi_i$. Я не стала обозначать их индексами, т.к. они все равны 1/3. Т.е. с другой стороны,можно составит систему, где каждая строчка матрицы равна единице и уже потом доказывать, что элементы равны?

Получится,что:

$$ \left\{ \begin{array}{rcll} p_{12}+p_{13}=1\\ p_{21}+p_{23}=1\\ p_{31}+p_{32}=1\\ \end{array} \right. $$

Тогда, если использовать систему из предыдущего сообщения, получится, что:
$p_{21}+p_{31}=p_{21}+p_{23}$ => $p_{31}=p_{23}$
$p_{13}+p_{23}=p_{12}+p_{13}$ => $p_{23}=p_{12}$

И таким образом, $p_{31}=p_{12}=p_{23}$

Верно?

[--mS--]

Ну если получилось то, что требовалось доказать, то, наверное, верно?

[Polly_Molly]

Просто я была не уверена насчет того,правильно ли я применяла все формулы.
Спасибо!