В одной английской книге есть одна теорема. Одну половину этой теоремы не могу никак доказать. ("сигнатура" это "vocabulary".)
Предложение. Пусть

и

структуры на сигнатуре

Если функция

- вложение (сохраняет все литералы), то

- подструктура

Итак, надо доказать три условия.
1.

и

имеют одну и ту же сигнатуру (Выполняется.)
2.

(Мне кажется и это можно показать.)
3.

и

интерпретируют

на
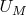
одинаковым образом.
И вот третий пункт не получается. Не понимаю почему константы из

должны интерпретироваться одинаково?