Категории и функторы

[lampard]

Помогите, пожалуйста, понять аксиому для категорий.

Аксиома 1. Два множества $\Mor(A,B)$ и $\Mor(A',B')$ не пересекаются, за исключением случая $A=A'$ и $B=B'$. В этом случае они равны.

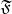
Пусть $\mathfrak{F}$ - категория, объектами которой служат множества, а морфизмами - отображения множеств. Аксиома 1 тривиальным образом удовлетворяется.

А как это она тривиальным образом удовлетворяется - что-то не пойму?

[Xaositect]

А там перед этим нигде не определяется отображение множеств?
По всей видимости, используется определение по Бурбаки: функцией называется тройка $(X, \Gamma, Y)$, где $X$ и $Y$ --- множества, а $\Gamma$ --- функциональное отношение на $X\times Y$ (график функции), т.е. подмножество $X\times Y$ такое, что $(x, y_1)\in \Gamma, (x, y_2)\in \Gamma \Rightarrow y_1 = y_2$.