Берем любое

. При


Берём

и рассмотрим посл-ть

.

возрастает и неограничена (иначе для предела выполнялось бы
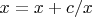
). Поэтому

, значит,

.
Поскольку

и

, то существует предел

Итак,

для некоторого

(

). Подставляем это в тождество из условия, получим

Тогда функция

удовлетворяет

Тогда

, поэтому

при

. Учитывая

, получаем

. Осталось из этого барахла выбрать монотонные функции.