Матричное умножение

[schoolboy1]

В учебнике Коренева Г.В. на стр.19 непонятное место.После рассмотрения тождества Эйлера-Лагранжа в индесной форме, предложено упражнение (2.19), где нужно выполнить матричное умножение. Выполнил, знак всех элементов (в произведении) получил прямо противоположный, где в учебнике плюс- там у меня минус и наоборот.
На той же странице речь идёт о том, что матрицы транспонированы.
Вопрос1.: Откуда это видно, что они транспонированы?
Вопрос2.:Почему указано, что надо умножать строку на строку, а не строку на столбец?
Даже если бы они и были транспонированы, то надо умножать как и положено-строку на столбец.Коренев Г.В. — Тензорное исчисление

[AKM]

Тема перемещена из форума «Математика (общие вопросы)» в форум «Помогите решить / разобраться (М)»
Причина переноса: не указана.

[Munin]

Дело в том, что там как раз надо выполнить НЕ матричное умножение. Перемножаемые объекты - не матрицы, а тензоры. Для матриц правило умножения всегда "строка на столбец". Это связано с тем, что элемент матрицы жёстко указан своим положением: такая-то строка и такой-то столбец. А для тензоров элемент жёстко указан своими индексами, которых вообще больше двух. Это последовательность чисел: такой-то первый индекс, такой-то второй индекс, такой-то третий индекс... Расположение элементов тензора в табличку наподобие матрицы - только вспомогательное действие, тензор остаётся самим собой, пока мы не перепутали его элементов именно по индексам.

Я рекомендую (пока не появится привычки, да и потом это полезно бывает) чтобы не запутаться, не просто писать тензоры "как матрицы", но ещё и отмечать, какой индекс где изменяется: какой индекс соответствует номеру строки, а какой номеру столбца. Тогда формула будет выглядеть так:

$$a_{is}a_{ks}=\begin{array}{cc}i\,\diagdown s&\\&\left[\begin{array}{rrr}0_{\phantom{0}}&a_3&-a_2\\-a_3&0_{\phantom{0}}&a_1\\a_2&-a_1&0_{\phantom{0}}\end{array}\right]\cdot\end{array}\begin{array}{cc}k\diagdown s&\\&\left[\begin{array}{rrr}0_{\phantom{0}}&a_3&-a_2\\-a_3&0_{\phantom{0}}&a_1\\a_2&-a_1&0_{\phantom{0}}\end{array}\right]\end{array}=\ldots$$

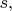
Теперь должно быть видно, что имеет в виду Коренев: индекс $s,$ по которому нужно сворачивать, и там и там пробегает по строке, так что перемножать надо строку на строку. Но это связано просто с тем, что мы записали тензоры в привычном виде "первый индекс по вертикали, второй по горизонтали". А могли бы и наоборот, "транспонировать" якобы-матрицу для второго тензора, тогда запись бы поменялась, зато произведение бралось бы по привычному рецепту "строка на столбец", и вот это записано у Коренева:

$$a_{is}a_{ks}=\begin{array}{cc}i\,\diagdown s&\\&\left[\begin{array}{rrr}0_{\phantom{0}}&a_3&-a_2\\-a_3&0_{\phantom{0}}&a_1\\a_2&-a_1&0_{\phantom{0}}\end{array}\right]\cdot\end{array}\begin{array}{cc}s\diagdown k&\\&\left[\begin{array}{rrr}0_{\phantom{0}}&-a_3&a_2\\a_3&0_{\phantom{0}}&-a_1\\-a_2&a_1&0_{\phantom{0}}\end{array}\right]\end{array}=\ldots$$

С тензорами и то и то допустимо, потому что нет жёстких правил, как записывать тензоры "как матрицы", и нет жёстких правил умножения в терминах строк и столбцов, а жёсткие правила относятся к тому, какой индекс на котором месте стоит, и какой с каким перемножается (сворачивается). Здесь структура того, что надо посчитать, сводится к тому, что надо свернуть второй индекс со вторым, а как вы это расположите на листке бумаги - безразлично. Можно вообще не рисовать "матриц", а выписывать по одному элементу, типа скучного столбика:

$a_{1s}a_{1s}=a_pa_p\delta_{11}-a_1a_1=a_1^1+a_2^1+a_3^2-a_1^2=a_2^1+a_3^2$
$a_{1s}a_{2s}=a_pa_p\delta_{12}-a_1a_2=0-a_1a_2=-a_1a_2$
...
$a_{2s}a_{1s}=a_pa_p\delta_{22}-a_2a_2=a_1^1+a_2^1+a_3^2-a_2^2=a_1^1+a_3^2$
...