Найти все значения для которых последовательность сходится

[xmaister]

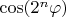
Задача такая (№3): Пусть $f(x)=4x-x^2$ Рассмотрим последовательность $x_{n+1}=f(x_n)$. Найти все $x_0\in [0,1]$ для которых последовательность сходится. Нехитрыми преобразованиями будем иметь $x_n=2(1-\cos (2^n\varphi))$, где $\varphi$ зависит от $x_0$. Т.е. задача свелась к нахождению всех $\frac{\pi}{3}\le\varphi\le\frac{\pi}{2}$ для коотрых $\cos (2^n\varphi)$- сходится. Но я не могу проверить сходимость даже для $\varphi=1$. Подскажите, как это сделать? Понятно, что если $\cos 2^n$- сходится, то сходится к $1$ или $-\frac{1}{2}$. Предположим, что сходится к данным числам то что можно получить?

[ИСН]

Опечатка: $f(x)=4(x-x^2)$, конечно.

-- Ср, 2012-11-14, 18:19 --

впрочем один хрен

[xmaister]

ИСН
С чего Вы взяли, то опечатка? Чем плоха задача в исходной постановке?

-- 14.11.2012, 18:20 --

Тут проблема в том, что не умею оценивать такие быстро растущие тригонометрические суммы.

[ИСН]

Задача в исходной постановке плоха тем, что иксы пляшут от 0 до 4, а нас спрашивают что-то про [0,1].

-- Ср, 2012-11-14, 18:23 --

(Это не противоречит ничему, а только кагбе намекает.)

[xmaister]

Ну ОК, давайте оставим исходную постановку. Есть мысль, что эта последовательность для почти всех $x_0\in [0,1]$. Можно ли доказать хотя бы это?

[nnosipov]

Загляните сюда: topic53461.html

[xmaister]

Почитал, ответа на вопрос не вижу.

[ex-math]

Если $\varphi=\pi\alpha$, где $\alpha$ -- рациональное со знаменателем, равным степени двойки (м.б. нулевой), то $\cos(2^n\varphi)$ стремится к 1. Если знаменатель $\alpha$ не равен степени двойки, предела не будет.
Осталось понять, что будет для иррациональных $\alpha$.

[xmaister]

ex-math в сообщении #645055 писал(а):

Если знаменатель $\alpha$ не равен степени двойки, предела не будет.

А как же $\alpha=\frac{1}{3}$?

[ex-math]

Да, с синусом перепутал.
Вообще надо $\alpha$ в двоичную дробь раскладывать, видимо.

[ИСН]

ex-math в сообщении #645064 писал(а):

в двоичную дробь раскладывать

Собственно, это и есть ответ. Если там с какого-то места сплошь единицы или сплошь нули (что, в сущности, одно и то же) - это случай сходимости, описанный выше. Если с какого-то места период, то у нас угол выходит на период. Тот может быть любой длины. Период 2 имеет ту особенность, что...