Периметры вложенных выпуклых фигур

[ewert]

ex-math в сообщении #642928 писал(а):

Но монотонную зависимость периметра от вложенности что-то никак не угляжу. Здесь как-то еще замкнутость ломаной должна быть задействована.

Конечно, должна -- и тогда монотонность тривиальна.

Пусть один выпуклый многоугольник вложен в другой. Проводим прямую через одну из сторон внутреннего многоугольника и отсекаем этой прямой ту часть внешнего многоугольника, которая не содержит внутреннего -- периметр внешнего многоугольника при этом разве что уменьшится. И так перебираем все стороны внутреннего многоугольника, пока не урежем внешний многоугольник до внутреннего.

[Oleg Zubelevich]

Вопрос Профессор Снэйп очевиден с самого начала. Это один из очевидных вопросов, строгое решение которых требует предельной аккуратности и техники и не является коротким. Поэтому спекуляции некоторых так называемых "заслуженных участников" по поводу очевидности , тривиальности и т.п. выглядят глупо. Тут надо либо выложить строгое доказательство со всеми подробностями или помалкивать.

[ewert]

Oleg Zubelevich в сообщении #642944 писал(а):

Это один из очевидных вопросов, строгое решение которых требует предельной аккуратности и техники и не является коротким.

Какая кривая называется спрямляемой?

[Oleg Zubelevich]

не знаете -- откройте учебник

[ex-math]

ewert
Так вот почему мне предложение Nemiroff с касательными покоя не давало --- это ровно оно и есть, только без ненужной шелухи с существованием касательных и бесконечностью последовательности множеств.

[ewert]

Oleg Zubelevich в сообщении #642952 писал(а):

не знаете -- откройте учебник

Я знаю. Что Вы понимаете под спрямляемой кривой?

-- Вс ноя 11, 2012 15:34:40 --

ex-math в сообщении #642959 писал(а):

Так вот почему мне предложение Nemiroff с касательными покоя не давало --- это ровно оно и есть, только без ненужной шелухи с существованием касательных и бесконечностью последовательности множеств.

Предложение Nemiroff крайне неудачно для доказательства монотонности длин вложенных кривых -- слишком много заклинаний понадобится. Но зато оно даёт полезный завершающий штрих -- оно доказывает строгую монотонность длин в зависимости от строгой вложенности (если, конечно, считать оба множества открытыми или оба замкнутыми -- в общем, как-то определиться с границами).

[Oleg Zubelevich]

ewert в сообщении #642960 писал(а):

Я знаю. Что Вы понимаете под спрямляемой кривой?

Типа поэкзаменовать меня решили. Ну-ну.
Кстати, у Вас нет еще кривой. Ваше "доказательство" неявно исходит из того, что локально граница выпуклого множества является графиком функции. Что само по себе надо доказывать. Это именно те подробности о которых я и намекал, а Вы их так и не увидели. Думаю, что есть и другие нюансы. Так, что пишите доказательство. Остальное -- треп.

[ewert]

Oleg Zubelevich в сообщении #642977 писал(а):

Ваше "доказательство" неявно исходит из того, что локально граница выпуклого множества является графиком функции. Что само по себе надо доказывать.

Совершенно верно. Однако это утверждение родственно тому факту, что любая выпуклая функция непрерывна. Последний факт действительно нетривиален, но он настолько фундаментален сам по себе, что доказывать его ещё раз в рамках данной задачи довольно нелепо.

Ну пожалуйста, специально для Вас. Фиксируем любую внутреннюю точку $O$ и сопоставляем каждому выходящему из неё лучу конец максимального интервала луча, лежащего в данном множестве; будем называть такие точки максимальными. Необходимо доказать, что зависимость максимальной точки от положения луча непрерывна (тогда множество максимальных точек автоматически образует границу). Что ж, предположим, что для некоторой максимальной точки $M$ непрерывность нарушается, и для определённости предположим, что она нарушается слева. Т.е. 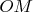существует последовательность максимальных точек $N_k$, стягивающихся слева от луча к точке $K$, лежащей на луче $OM$, но не совпадающей с $M$. 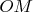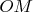Если $K$ оказывается внутри интервала $OM$, то выпуклость множества нарушается на отрезке $LM$, где $L$ -- некоторая точка множества слева от луча $OM$ (поскольку при достаточно больших $k$ луч $ON_k$ пересекает этот отрезок своей "внешней" частью, т.е. не содержащей точек множества). 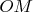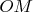Если же, наоборот, $K$ оказывается вне отрезка $OM$, то по аналогичным причинам выпуклость нарушается на отрезках $N_kL$, где $L$ -- какая-либо фиксированная точка множества справа от луча $OM$ (поскольку теперь уже этот луч пересекает отрезки $N_kL$ своей внешней частью при достаточно больших $k$).

И что, стоило городить этот общеизвестный огород?

[Oleg Zubelevich]

Я сразу сказал, что утверждение очевидно, но доказательство его требует аккуратности. Добавлю: четкого понимания, что надо доказывать. Вот , например,

ewert в сообщении #643038 писал(а):

Фиксируем любую внутреннюю точку $O$ и сопоставляем каждому выходящему из неё лучу конец максимального интервала луча, лежащего в данном множестве; будем называть такие точки максимальными. Необходимо доказать, что зависимость максимальной точки от положения луча непрерывна (тогда множество максимальных точек автоматически образует границу).

вот с какой радости "автоматически"? Скорее всего для невыпуклых множеств это автоматически неверно. А выпуклостью Вы не воспользовались. Ну и так далее по тексту

[ewert]

Oleg Zubelevich в сообщении #643156 писал(а):

Скорее всего для невыпуклых множеств это автоматически неверно. А выпуклостью Вы не воспользовались.

Зато воспользовался очевидной звёздностью области, чего и достаточно и при которой непрерывности очевидно достаточно. Что, все банальности надо разжёвывать?

[Oleg Zubelevich]

ewert в сообщении #643171 писал(а):

Зато воспользовался очевидной звёздностью области

докажите звездность

[ewert]

Oleg Zubelevich в сообщении #643193 писал(а):

докажите звездность

тривиальное следствие выпуклости

[Oleg Zubelevich]

ewert в сообщении #643359 писал(а):

Oleg Zubelevich в сообщении #643193 писал(а):

докажите звездность

тривиальное следствие выпуклости

Про тривальность все уже слышали сто раз. Доказательство где?

[Doil-byle]

(Оффтоп)

В выпуклом множестве любой отрезок, соединяющий любые две точки данного множества принадлежит этому множеству. В звёздном множестве $D $ $\exists$ $(.)$ $k$, такая, что для любого отрезка $[k,x]$, соединяющего точку $k$ с произвольной точкой $x \in D$, $[k,x] \in D$. Значит выпуклое множество - частный случай звёздного множества, разве не так? Хотя, я, вообще, нуб, и мне стыдно вставлять фразу в это обсуждение.

[Oleg Zubelevich]

(Оффтоп)

Doil-byle в сообщении #643467 писал(а):

В звёздном множестве $D $ $\exists$ $(.)$ $k$, такая, что для любого отрезка $[k,x]$, соединяющего точку $k$ с произвольной точкой $x \in D$, $[k,x] \in D$

такое определение звездности ewertу не поможет