Многочлен это последовательность комплексных чисел
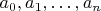
. Можно считать, что эта последовательность бесконечна (следующие члены равны нулю):

. Последовательность комплексных чисел — это и есть отображение

,

. Поэтому
![$\mathbb C[x]$ $\mathbb C[x]$](https://dxdy-01.korotkov.co.uk/f/c/d/d/cddc00cbbe3ffeae6c137340536a2e6682.png)
есть пространство отображений

, равных нулю почти всюду. Если теперь имеется такая последовательность

и совершенно произвольная последовательность

, то

можно рассматривать как функционал на
![$\mathbb C[x]$ $\mathbb C[x]$](https://dxdy-01.korotkov.co.uk/f/c/d/d/cddc00cbbe3ffeae6c137340536a2e6682.png)
, сопоставляющий последовательности

число

.