Прошу прощение в случае Гейзенберга группа а не алгебра,задается соотношениями:
Нашел ее определение:





,где

-простое число
Прошу помочь найти ее представления.
P.S: В случае Гекке точно алгебра,тоже хочется найти ее представления и вообще почитать про нее,как я уже говорил. К эта алгебра возникает при рассмотрении представлений группы

,где
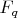
поле из

элементов, может уж где почитать про представления этой группы кто нибудь знает?