Понятно, что каждый морфизм в любой категории должен «помнить» свою область определения и область значений.
Да, это я понимаю. Это же одна из аксиом категории. В теории множеств отображение

определяют как

,

-график. Это тоже я понимаю. Если бы в категории

объектами были бы множествами с какой-то структурой то да, вопросов бы не возникло...
Иногда говорят, что все
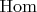
должны быть дизъюнктны — ну, хорошо; иногда говорят, что морфизм

— это тройка

. Тоже метод.
Как понимать упорядоченную тройку

где

- непонятно какие объекты непонятно какой категории?
После этого предлагается забыть об этих деталях и просто принять, что если вы берете какой-то морфизм, то Вы знаете, откуда и куда он действует. В Вашем случае с категорией морфизмов — ну, может быть, так получилось, что одну и ту же пару

можно рассматривать и как морфизм из

в

, и как морфизм из

в

. И что? Никому от этого хуже не стало, вроде бы.
Так никакой категории морфизмов ещё нет, ну по крайней мере я не доказал, что моорфизмы образуют категорию.

Вот мне не ясно, почему

образует категорию.