In the acute-angled triangle

-
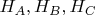
are feets of the peprendiculars from the vertices

to the corresponding sides respectively.

and

are the feets of the perpendiculars from
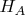
to
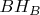
and
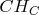
respectively.

and

are feets of the perpendiculars from
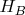
to
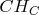
and
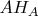
respectively.

and

are the feets of the perpendiculars from
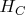
to
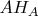
and
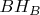
respectively. Prove that
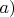
If

and

are the feets of the perpendiculars from
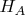
and
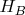
to

then points
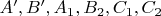
are concylic.
If
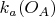
is the circle through
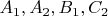
;
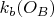
is the circle through
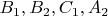
;
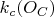
is the circle through
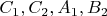
; then circumradii of the triangles
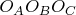
and
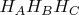
are equal.