Алгоритм для нахождения минимальной суммы (аля рюкзак)

[mishanya]

Помогите,пожалуйста,решить следующую задачу

$$\text{Входные данные:} \text{массив списков }({P_i, Q_i, R_i, F_i}) \text{и } {L} \text{,все натуральные большие либо равные нулю}$$ $${C_i}=\begin{cases} {P_i \cdot L_i},&\text{если } {L_i<R_i \leqslant F_i;}\\ {Q_i \cdot L_i},&\text{если } {F_i \geqslant L_i \geqslant R_i };}\\ \end{cases}\\ $$ $$min({\sum^{N}_{i=0} {C_i}}) \text{=? } \text{при условии } {\sum {L_i} \geqslant {L}} $$ $$\text{т.е по сути надо найти набор L-итых сумма которых больше L и при которых суммарная С будет min}$$

[sup]

Попробуйте вместо одной переменной $L_i$ ввести две переменных $L^1_i, L^2_i$ с условиями
$L^1_i <R_i$
$R_i \leqslant L^2_i \leqslant F_i$
И минимизировать
$\sum P_iL^1_i +Q_iL^2_i$
при условии
$\sum L^1_i +L^2_i \geqslant L$

[Cash]

Идея такая:
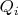
Массив из $Q_i, P_i$ отсортировать по возрастанию. Тогда последовательно проходим по массиву и берем максимально возможные $L_i$, пока не наберем $L$. Там остаются тонкости - когда отказываться от $P_i$ в пользу $Q_i$ - здесь простое соотношение, а также набор непосредственно вблизи границы, кроме перебора пока ничего не вижу, но даже перебор здесь будет небольшой.