Сходимость цепей Маркова

[alisa-lebovski]

Пусть X^{(N)}_n$ - последовательность эргодических цепей Маркова ($N$ - номер цепи в последовательности) на $R$, и ${\tilde X}^{(N)}$ - случайные величины с соответствующими стационарными распределениями. Пусть $(X^{(N)}_n|X^{(N)}_{n-1}=u)\to f(u)$, $N\to\infty$, т.е. есть в каком-то смысле сходимость к детерминированной последовательности $u_n=f(u_{n-1})$, и существует неподвижная точка $u^*=f(u^*)$. 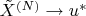При каких условиях верно, что ${\tilde X}^{(N)}\to u^*$ по вероятности при $N\to\infty$? И что происходит, если неподвижных точек несколько?