
Несколько тривиальных соображений:
1) Из-за члена с

и логарифма, ООФ не шире
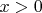
2) Из-за

и, опять-таки логарифма, при

функция не определена.
3) Соответственно, имеет место быть особенность при

.
4) Первую прикидку поведения можно получить, рассмотрев пределы при стремлении к

Ну а дальше — исследование функции с помощью производной

Последующее — просто глядя на графики (и потому неподтверждено ну никак):
а) при

монотонно растет
б) В целом, при

график имеет

образную форму. Существует критическое значение, при котором вершина касается 0. При большем

вершина меньше 0, при меньшем — больше.