Let
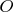
and

are the incenter and intersection points of the diagonals of the circumscribed quadrilateral

respectively. Though

is drawn line

, perpendicular to
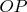
.

and

are the intersection points of

with the sides of

. Prove that

is the middle of

.
(Оффтоп)
This problem is too easy. Only inscribed quadrilaterals and Brianchon theorem solves it.