Плотность распределения компонент вектора

[Measure]

Задача:
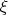
Случайные величины $\xi $ и $ \eta $ имеют плотности распределении f (x) и g(х) и функции pаcпредeлeния $F(x)$ и $G (х)$ соответственно.
Случайный вектор $ \zeta = (\zeta_1, \zeta_2) $ имеет плотность распределения $p(x, y)= f(x)g(y)(1+r(F(x), G(y)))$ , где функция $r (x, y) $ удовлетворяет условиям:
1. $\min r (u, v) dv \geqslant -1, $ минимум берется по $u, v: 0\leqslant u, v \leqslant 1$
2. $\int_0^1 r (u, v) dv = \int_0^1 r (u, v) du = 0$
Найти плотности $ p_1 $и $p_2 $ распределения компонент $\zeta_1 $ и $\zeta_2$ вектора $\zeta$.

Попытка решения:
$p_1(x) = \int_{-\infty}^{\infty} p(x, y) dy = \int_{-\infty}^{\infty} f(x)g(y) (1 + r(F(x), G(y))) dy = \int_{-\infty}^{\infty} f(x)g(y)dy + \int_{-\infty}^{\infty} f(x)g(y)r(F(x), G(y))dy = f(x) + f(x) \int_{-\infty}^{\infty}g(y)r(F(x), G(y))dy = f(x) + f(x) \int_{-\infty}^{\infty}r(F(x), G(y))dG(y) = f(x) $

Подскажите, пожалуйста, в чем моя ошибка и как использовать условие 1?

[--mS--]

Ни в чём. Условие (1) уже использовано для неотрицательности, иначе указанная совместная плотность - не плотность. Ответ, естественно, правильный. Выводы только следует правильные сделать из этого известного примера, вот и всё.

[Measure]

Спасибо!