Вложенность множеств

[Женисбек]

Пусть $f_n(x)=\sqrt{n}x\ln\left(1+\frac{x}{\sqrt{n}}\right)$
Если разложить логарифм в ряд Тейлора, можно показать, что $f_n(x)\to x^2,\ n\to+\infty$
Пусть далее
$[a_n,b_n]=\{x: f_n(x)\le1\}$
и пусть $f_n(c)\le1$. Как показать, что
$\left(c-\frac{a_n+b_n}{2}\right)^2\le1$
?

[ewert]

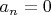
Все функции монотонно возрастают от нуля до бесконечности, поэтому $a_n=0$. Если $t_n=\dfrac{b_n}{\sqrt n}$, то $t_n\ln(1+t_n)=\dfrac1n$, откуда $t_n\sim\dfrac{1}{\sqrt n}$ и, соответственно, $b_n\to1$. Но это неважно, а важно, что $b_n$ монотонно убывают (например, потому, что если $F(x,m)=mx\ln(1+\frac xm)=1$, то $\dfrac{dx}{dm}=-\dfrac{F'_m}{F'_x}>0$). Т.е. достаточно было бы того , что $b_1<2$, фактически же даже явно $b_1<\frac32$.

[Женисбек]

ewert в сообщении #603509 писал(а):

Все функции монотонно возрастают от нуля до бесконечности, поэтому $a_n=0$.

Но ведь $f_n(x)$ монотонно убывают на $(-\sqrt{n},0)$ от $+\infty$ до $0$. Поэтому $a_n<0$...