Обобщённый шахматный конь

[Ktina]

Обобщённый шахматный конь (или $(n, m)\text{-конь}$) - шахматная фигура, ход которой - это прыжок на $n$ клеток по вертикали или по горизонтали, а затем - на $m$ клеток в перпендикулярном направлении (при $n=2, m=1$ имеем обычного шахматного коня).

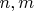
Доказать, что для любых натуральных $n, m$ можно раскрасить бесконечную шахматную доску в два цвета так, чтобы любые две клетки, соединённые ходом $(n, m)\text{-коня}$ были покрашены в разные цвета.

[temp03]

(Всё это прошу учесть при решении задачи)

Обобщённый шахматный конь — суперсимметричный конь, который со всех сторон конь, как бы вы на него ни посмотрели.
Чтобы сесть на этого коня верхом, нужно найти седловую точку. Сопротивление коня в этом случае пренебрежимо мало. Координаты седловой точки, однако, являются комплексными.
Задача о причёсывании шерсти нечётномерного коня неразрешима.
Всякий односвязный компактный n-мерный конь без края гомеоморфен n-мерному сферическому коню.

[Dave]

(Здесь подробнее о таком коне)

Клац!

Не ограничивая общности, можно считать, что $n$ и $m$ взаимно просты. Если оба этих числа нечётные, то раскрашиваем чередующимися полосками (как зебру или арбуз) - обе координаты при ходе коня поменяют чётность, а при смене чётности одной из них поменяется и цвет клетки; а если среди $n$ и $m$ одно число чётное, а другое нечётное, то раскрашиваем доску в шахматном порядке - при ходе коня сумма координат поменяет чётность, а значит и цвет клетки тоже изменится.

[temp03]

(да...)

Dave, да, ваша информация существенно полнее.