комплексный интеграл

[igor520]

задача с вступительного в магистратуру НГУ, который прошел вчера утром
из 60 абитуриентов никто не решил, гы
найти значение интеграла
$\int \frac{1}{(z-2)\left(z^{2012}+1\right)} \, dz$
по контуру
$\frac{x^2}{4}+\frac{y^2}{2}=1$
где
$z=x+i y$

[ex-math]

Строго говоря, такой интеграл не существует. Его можно вычислить только в смысле главного значения, то есть взяв предел при $\varepsilon$, стремящемся к нулю, интеграла по участку контура, лежащему вне $\varepsilon$-окрестности точки $z=2$.

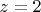
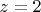
Если замкнуть этот контур частью окружности $|z-2|=\varepsilon$, захватив точку $z=2$, то интеграл по такому контуру будет равен нулю, а часть окружности нужно параметризовать и посмотреть, к чему будет стремиться интеграл по ней.

У меня получился ответ $-\dfrac{\pi i}{2^{2012}+1}$.

[igor520]

а что происходит с частью интеграла, связанного с
$\frac{1}{z^{2012}+1}$
если решить уравнение $z^{2012}+1=0$, то получается 2012 особых точек на единичной окружности.... разве наличие этих точек не влияет на значение интеграла?

[ex-math]

Вычет в бесконечности равен нулю. С другой стороны, он равен минус сумме вычетов во всех конечных особых точках.