найти объем тела, ограниченного поверхностью

[igor520]

Задача из вступительных в НГУ уровня магистратуры:
Найти объем тела, ограниченного поверхностью $(x+y/2+z/3)^2=x+y$ и координатными плоскостями. Дополнительное условие $x,y,z \geqslant0$.

Попытка решения - выделить функцию $z(x,y)$, затем проинтегрировать по $x$ и $y$. Но должно быть более элегантное решение, т.к. задача должна решаться минут за 30-60 без компьютера. Возможно, что нужно сделать линейное преобразование координат, затем решить задачу в других координатах. Если кто-нибудь знает как это решается, пожалуйста напишите.

[Nacuott]

Заданная поверхность - это параболический цилиндр (наклоненный).Если его поставить вертикально (повернув соответствующим образом и плоскости), чтобы образующие были параллельны оси Z , то интегрирование выполнится легко.
Простого способа нахождения объема не видно (по крайней мере, мне). Этот объем равен 1.5 куб.ед.

[igor520]

ок, спасибо...... у меня получился тот же результат - 1.5

[svv]

Скажите, а что значит "уровня магистратуры", какова подготовка людей, сдающих эти экзамены?

[igor520]

Задача со вступительных экзаменов в магистратуру, т.е. подготовка - 5 лет учебы на механико-математическом факультете.

[igor520]

ок, чтобы это решить нужно заменить координаты
$u=x$
$v=x+y$
$w=x+y/2+z/3$
тогда уравнение поверхности сводится к $w^2=v$, причем очень удачно независящее от $u$
ограничивающие плоскости становятся следующими:
$u=0$
$v-u=0$
$w-u/2-v/2=0$
если это все начертить в новых координатах $uvw$, то можно заметить, что $u$ принимает значения от 0 до 1, а "срезы по $u$" имеют вид параболы отсеченной прямой
площадь отсеченного участка выражается через интеграл по $dv$ или по $dw$
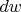
при интегрировании нужно не забыть про якобиан, который равен 3 в данном случае