Лучше опустить бессмысленную конструкцию "множество В от k не зависит", это же не функция. И по-моему, вот это утверждение
Цитата:
является выражением дистрибутивности кванторов и по степени тривиальности эквивалентно утверждению теоремы. То есть это просто ее перевод. Следует теперь, например, просто рассмотреть случаи, когда
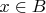
и обратное.