Dima1234Следующий этап -- учёт всех замечаний -- тех, что были сделаны, и ещё моих.
0) Код
sin даёт некрасивый

, код
\sin даёт красивый

. Аналогично
\cos,
\pi:

,

.
1) Так как в уравнение окружности

радиус входит в квадрате,

-- это окружность радиуса

, а не

.
2) Полярный угол лучше обозначать

(код
\varphi), Вас будут лучше понимать. Угол

-- это в сферических координатах.
3)

Вы заменили на

, а правильно

.
4)

-- немедленно упростить до одной буквы. Инстинкт упрощения и приведения в порядок должен быть в крови.
5) Пределы

неправильные. Исправьте их с учетом условия
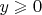
.
6) Когда пределы интегрирования найдены, уже не обозначайте область интегрирования буквой. Буква, кстати, если уж её писать, будет та же (

) и в полярных: область не изменилась. Вместо этого напишите при каждом интеграле пределы интегрирования, вроде такого:

, или просто

, если понятно, по какой переменной берется интеграл.