Решение уравнения движения пучка электронов

[Aznor]

Мне надо решить вот такую задачу:
есть пучок электронов с начальными координатами и импульсом, движущегося в ускорителе.
Я написал уравнение движение для данного случая, но дело в том. что на установке есть и промежутки где нет полей внешних. И из за этого приходится решать одно и то же уравнение много раз, что очень не хорошо.........
Вопрос, можно ли написать, файл-функцию, которая будет решать уравнение движения пучка при любых полях Е и Н и выдавать выходные данные, которые будут являться начальными условиями ко входу в следующую секцию установки???
Я недавно только начал изучать MATLAB, поэтому буду рад любой помощи, и разъяснению, чтобы я смог понять и в будущем мог это все использовать.

Вот начало моей программы и уравнение движения (в прикрепленном файле, система (1)), для которого хочу написать файл - функцию.


clc
clear all;
% число частиц
N=500;
% все в метрах (это все промежутки установки)
L1=0.5; L2=3; L3=0.5; L4=3; L5=0.5; L6=3; L7=0.5; L8=2;
%начальные координаты, пусть пучок распределен по гауссу в любом поперечнике с характерными размерами a b c (интервал в котором будет большинство координат, потом на графике видно будет)
a=10^(-5);b=2*10^(-5);c=3*10^(-5);
x(1,:)=a*randn(1,N);
y(1,:)=b*randn(1,N);
z(1,:)=c*randn(1,N);
plot3(x,y,z,'.')
% начальные импульсы в диапазоне p1,p2,p3 и тоже по гауссу
p1=10;p2=20;p3=30;
px(1,:)=p1*rand(1,N);
py(1,:)=p2*rand(1,N);
pz(1,:)=p3*rand(1,N);
%открываем цикл по частицам
for i=1:N;
%берем i-ю частицу с соответствующими начальными условиями
x0=x(1,i);
y0=y(1,i);
z0=z(1,i);
p0=px(1,i);
p0=py(1,i);
p0=pz(1,i);
%далее решаем уравнения движения (система (1))
????

z(1,:)<=L1;
% запоминаем все решения, чтобы потом можно было их использовать в визуализации
?????

[photon]

Aznor в сообщении #575295 писал(а):

Вот начало моей программы и уравнение движения (в прикрепленном файле, система (1)), для которого хочу написать файл - функцию.

Нет тут никакого прикрепленного файла.

Я думаю, здесь неважно, какой вид имеют те или иные Ваши уравнения - будет проще понять, что Вам нужно (я, если честно, не понял) и помочь Вам, если Вы для начала запишете в общем виде, типа: имеется функция такая-то, входные аргументы такие-то, меняться должны так-то, на выходе надо получить то-то.

[Aznor]

\documentclass[12pt]{article}

\usepackage[utf8]{inputenc}


\usepackage{geometry}
\geometry{a4paper}

\usepackage{graphicx}


\usepackage{booktabs}
\usepackage{array}
\usepackage{paralist}
\usepackage{verbatim}
\usepackage{subfig}
\usepackage{fancyhdr}
\pagestyle{fancy}
\renewcommand{\headrulewidth}{0pt}
\lhead{}\chead{}\rhead{}
\lfoot{}\cfoot{\thepage}\rfoot{}

\usepackage[russian]{babel}
\usepackage[T2A]{fontenc}

\usepackage{sectsty}
\allsectionsfont{\sffamily\mdseries\upshape}


\usepackage[nottoc,notlof,notlot]{tocbibind}
\usepackage[titles,subfigure]{tocloft}
\renewcommand{\cftsecfont}{\rmfamily\mdseries\upshape}
\renewcommand{\cftsecpagefont}{\rmfamily\mdseries\upshape}



\title{Транспортировка пучка}


\begin{document}
\section{Начальные условия пучок}
Имеем систему, где взаимодействие частиц с полем не учитывается на данном участке, в этой системе тогда задаем число электронов $N$ и задаем соответственно начальные условия для всех электронов: начальные положения в пространстве $x_{i_0},y_{i_0},z_{i_0}$, начальные импульсы (или скорости) $p_{ix_0},p_{iy_0},p_{iz_0}$ для всех частиц $i=1,...,N$
Для большей правдопдобности. Пучок какое то время летит в отсутствии поля. Пусть он пролетает расстояние $L_1$ (от ВЧ пушки до Первого ускоряющего промежутка AC1) в котором нет внешних полей. Решаешь систему уравнений движения для каждой частицы ($i=1,..,N$) с соответствующими начальными условиями:

\begin{equation}
\label{1}\left\{\begin{array}{l} \dot{p}_{ix}=eE_x+e\left(\vec{v}\times\vec{H}\right)_{x}/c \\ [0.3cm] \dot{p}_{iy}=eE_y+e\left(\vec{v}\times\vec{H}\right)_{y}/c\\ [0.3cm] \dot{p}_{iz}=eE_z+e\left(\vec{v}\times\vec{H}\right)_{z}/c\\ [0.3cm] p_{ix}=\gamma mv_{ix}\\ [0.3cm] p_{iy}=\gamma mv_{iy}\\ [0.3cm] p_{iz}=\gamma mv_{iz}\\ [0.3cm] \dot{x}_{i}=v_{xi}\\ [0.3cm] \dot{y}_{i}=v_{yi}\\[0.3cm] \dot{z}_{i}=v_{zi} \end{array}\right.
\end{equation}

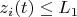
Т. к. в промежутке поля нет то правые части первых 3-х уравнений зануляются. Для каждой $i$-той частицы решаешь систему (1) до тех пор пока она не дойдет до первого ускоряющего промежутка (т. е. пока $z_i(t)\le L_1$). Как только она доходит до него запоминаем все значения координат и импульсов частицы $(x_i',y_i',z_i'=L_1),(p'_{ix},p'_{iy},p'_{iz})$ - это будут мои начальные условия для второго пункта, и перехожу ко второму пункту.


\section{Первый ускоряющий промежуток AC1}
Задаю поле в первом ускоряющем промежутке $\vec{E}_1=(E_{x},E_{y},E_{z})$ ( магнитного поля там нет $\vec{H}=(0,0,0)$). Решаю систему (1), но уже в качестве начальных условий беру конечные из первого пункта $(x_i',y_i',z_i'=L_1),(p'_{ix},p'_{iy},p'_{iz})$. Пусть длинна этого ускоряющего промежутка равна $L_2$, тогда решаю систему до тех пор пока $z_{i}(t)\le L_2$. Как только частица доходит до конца промежутка запоминаю ее конечные координаты и импульсы $(x_i'',y_i'',z_i''=L_2),(p''_{ix},p''_{iy},p''_{iz})$. После чего, опять же частица какое то время будет двигаться свободно до второго ускоряющего промежутка (пусть это расстояние равно $L_3$), возвращаешься к пункту 1 и решаю систему уравнений с нулевыми полями из 1, но в качестве начальных условий берешь уже $(x_i'',y_i'',z_i''=L_2),(p''_{ix},p''_{iy},p''_{iz})$. Как только частица доходит до вторго ускоряющего промежутка повторяешь процедуру этого пункта и т.д.


\end{document}