Équation

[gefest_md]

$x+\frac{\sin x}{x}=0$
How to solve this équation?

[svv]

Nihow, only chislenno.

[Алексей К.]

Ньюмерикалли.

(Опередили)

[gefest_md]

It is a school exercise about drawing the graphic of the function. What is numerically more exactly? I cannot find out the intersections with $Ox$ axis?

[Cash]

The equation $\sin{x} = -x^2$ have a one root on $(-1,0)$

[Алексей К.]

gefest_md в сообщении #574715 писал(а):

I cannot find out the intersections with $Ox$ axis?

You can not find this intersection exactly.
You can try to estimate it by graphical comparison of two plots, thoroughly traced.
You can plot two functions and perform graphic summation to get the result. I suppose, this is assumed as the solution.

[Munin]

gefest_md в сообщении #574715 писал(а):

It is a school exercise about drawing the graphic of the function.

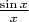
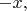
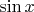
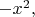
Then you should draw graphs of $\tfrac{\sin x}{x}$ and $-x,$ and then find their intersection points. Or, of $\sin x$ and $-x^2,$ as was proposed above.

gefest_md в сообщении #574715 писал(а):

What is numerically more exactly?

Numerical solution can be done with a number of methods, for example:
1. Start with some point, e. g. $x_0=-0.1.$
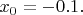
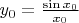
2. Calculate a $y_0=\tfrac{\sin x_0}{x_0}$ from it.
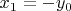
3. Assign $x_1=-y_0$ to be a next approximation.
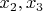
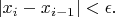
Repeat the steps 2 & 3 several times, proceeding to values $x_2,x_3$ and so on. If this process converges, stop when you reached the target precision, i. e. $\lvert x_i-x_{i-1}\rvert<\epsilon.$ There can be 'bad initial guesses' which lead to divergence, in such case try some other initial guess.