Здравствуйте.
Имеется ДУ:

, где

. Все функции являются вещественными.
Известно, что частное решение при

является периодическим. Требуется численно найти его период.
Как решать?
1. Находим общее решение

,
где

.
2. Можно найти половину периода, в данном случае будет совпадать со временем движения в течении которого фазовая траектория находится в положительной полуплоскости фазовой плоскости. Для этого нужно найти точку пересечения

фазовой траектории с осью абсцисс:

(1)
3. Зная точку

, можно найти период:

.
Проблема в том, что математические пакеты не хотят решать уравнение (1). Maple почему-то выдаёт комплексные корни, SciLab говорит, что решение расходится (не знаю, каким методом он пытается его решить).
Функции
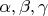
довольно громоздкие. Я приведу график интеграла как функции верхнего предела (1)

и её производной

Насколько видно из графиков, подобрать соответствующие коэффициенты для сходимости, скажем, алгоритма секущих вполне возможно.