Вот док-во неприводимости для

.
Допустим, что

. Можно считать, что
![$l,h\in\mathbb{Z}[x]$ $l,h\in\mathbb{Z}[x]$](https://dxdy-04.korotkov.co.uk/f/b/4/2/b42f292cb2d0fefa622d88daea3c73f982.png)
. Подстановка

дает

. Пусть для определенности

. Пусть

таково, что уравнение

имеет

(

) корней вида

, без потери общности, это

. Можно считать

, иначе рассмотрим разложение

. Тогда

,
![$u\in\mathbb{Z}[x]$ $u\in\mathbb{Z}[x]$](https://dxdy-01.korotkov.co.uk/f/c/2/8/c2863a860680a0586805297285cadcad82.png)
. Если

, то подстановка

дает

.
Такое равенство невозможно, т.к.

- различные целые числа и их не менее

.
Значит,

и, поскольку

, получаем

,

.
Тогда

и похожими рассуждениями получаем

,

.
Но тогда

приводим. Противоречие.
Возможно, некоторая модификация этих рассуждений пройдет и в случае

, но мне сразу ниче в голову не приходит. Но похожие рассуждения позволяют случай

свести к конечному перебору. Для этого достаточно заметить, что можно считать какое-то из

равным

(поскольку многочлены

и

при

одновременно приводимы/неприводимы). Тогда в приведенном выше рассуждении с

для

получаем конечное число возможностей.
Добавлено спустя 22 минуты 25 секунд:
xolms
А не могли бы Вы привести хотя бы идею док-ва для случая, когда дискриминант отрицателен.
Добавлено спустя 18 минут 9 секунд:
Для
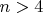
проходит то же док-во (с небольшим уточнением). А вот для

избавиться от перебора у меня не получается.