добрый день
мой вопрос из области акустики, но интересует именно математическая сторона. Есть ряд:

,
где

- заданные числа,

,

- заданное волновое число. Преобразование между прямоугольной и полярной с.к. задается формулами (в отличие от обычных - здесь абсцисса зависит от синуса, а ордината - от косинуса):

,
где

и

- заданные числа.
В статье говорится, что в полярной с.к. этот ряд будет иметь вид:

,
где

- функции Бесселя,

, фаза

.
Вопрос в математическом получении такого разложения для полярной с.к. По всем признакам оно получено с помощью применения теоремы сложения (см. Иванов Е.А. «Дифракция электромагнитных волн на двух телах»), но может я и ошибаюсь. Буду рад любой помощи.
PS.Геометрия и физика задачи такова:
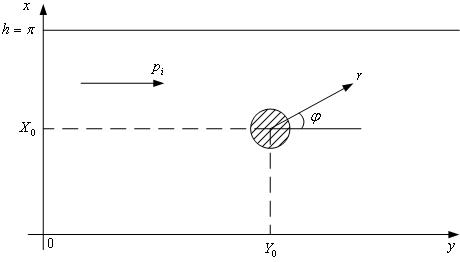
На тело в прямоугольном воноводе падает волна

, образованная заданным распределением источников, находящихся на расстоянии

от тела (цилиндр, образующая которого параллельна стенкам волновода и перпендикулярна оси картинки). Разложение, данное выше в прямоугольной с.к.,

является разложением падающей волны по собственным функциям волновода. Разложение

является разложением в полярной с.к., связанной с телом