Помогите, вроде всё делаю по алгоритму, но ответ получается неверный:
Условие: построить полярное разложение матрицы
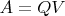
, где

- ортогональная, а

- симметричная неотрицательно-определённая, при
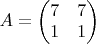
Моё решение:
1)
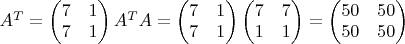
Собственные значения:
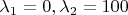
Из чего следует:
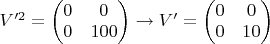
2) Находим

в базисе собственных векторов:

. Она будет иметь диагональный вид. От выбора собственных векторов ничего зависеть не должно, поэтому берём произвольные.
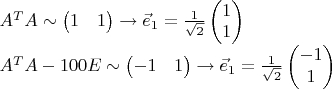
3) По матрице перехода восстанавливаем

в исходном базисе
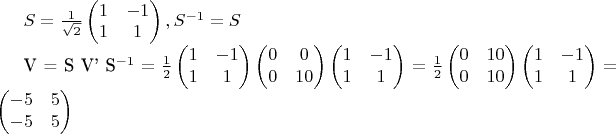
...которая не является ни симметричной, ни неотрицательно-определённой.
Что я делаю не так?