Электростатика. Метод зеркальных изображений.

[f3b4c9083ba91]

Добрый день!
Помогите пожайлуста разобраться с такой задачей:
Найти поле скалярного электрического потенциала системы зарядов у сферы:

Условия:
a = 2;
r1 = 3;{\gamma _1} = 30^\circ ;q1 = - 1;
r2 = 3;{\gamma _2} = 60^\circ ;q2 = 2;
r3 = 3;{\gamma _3} = 90^\circ ;q3 = - 1
Мое решение для первого заряда.

Формула для расчета
{U_c} = \frac{1}{{4\pi {\varepsilon _a}}}\left( {\frac{{{q_1}}}{{{r_1}}} + \frac{{{q_2}}}{{{r_2}}}} \right)
q2 это фиктивный заряд.
{x_2} = \frac{{{a^2}}}{{{x_1}}}

{q_2} = - {q_1}\frac{a}{{{x_1}}}

Вычисления:

{r_1} = \sqrt {{{\left( {{y_1} - {y_c}} \right)}^2} + {{\left( {{x_1} - {x_c}} \right)}^2}} = \sqrt {{{\left( {1.5 - 1.5} \right)}^2} + {{\left( {2.598 - 1.32} \right)}^2}} = 1.278

{r_2} = \sqrt {y_c^2 + {{\left( {{x_c} - {x_2}} \right)}^2}} = \sqrt {{{1.5}^2} + {{\left( {1.32 - 1.54} \right)}^2}} = 1.516

{x_2} = \frac{{{2^2}}}{{2.598}} = 1.54

{q_2} = - \left( { - 1} \right) \cdot \frac{3}{{2.598}} = 1.155


{U_c} = \frac{1}{{\frac{{4\pi \cdot {{10}^{ - 9}}}}{{36\pi }}}}\left( {\frac{{ - 1}}{{1.278}} + \frac{{1.155}}{{1.516}}} \right) = - 1.854 \cdot {10^8}
Очень надеюсь на вашу помощь.

[rustot]

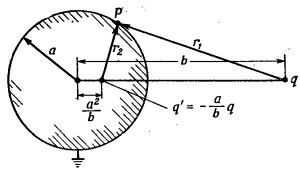
Вы как то странно расположили фиктивный заряд. Он на отрезке, соединяющем заряд с центром сферы должен быть.



Что такое "поле скалярного электрического потенциала" не понял. Функцию потенциала в любой точке от координат? Ну добавляете 3 фиктивных заряда и получите 6 слагаемых для любой точки вне сферы, а на поверхности и внутри всегда 0. А вы по-моему пытались посчитать потенциал самой сферы, не обратив внимания на то, что она заземлена.