Вкратце.
Теорема Луи Башелье.
Пусть дан процесс броуновского движения

.
Тогда для

сл. процессы

,

,
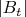
одинаково распределены и соот. функции совместной плотности вероятности имеют вид:


Сначала находим первую плотность, потом через нее выражаем вторую.
Так вот, пусть первая плотность найдена.
Тогда,

И дальше продолжаем преобразовывать данный интеграл к виду:
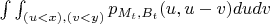
.
Верно ли мое предположение, что здесь была использована обычная замена:

?
И куда пропал знак?
Подскажите, пожалуйста.