Задача про плотность

[Babeuf]

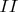
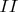
В области $x<0$ (область $I$) поддерживается стационарный разряд в магнитном поле ($H=1$ кЭ), направленном по оси $z$. Область $II$, примыкающая к активной зоне, образована двумя параллельными диэлетрическими пластинами, расположенными при $x=\frac {d} {2}$, $x=-\frac {d} {2}$ ($d=20$ см). За счёт амбиполярной диффузии плазма проникает из разряда в область $II$. Определить характерный масштаб спада плотности плазмы по оси $x$, если на границе $x=0$ распределние концентрации $n_0\cos(\frac {\pi z}{d})$. Давление нейтрального гелия, заполяющего оба объема - $0,1 Торр$, электронная температура плазмы - $2 эВ$ эВ, ионная - $0,2$ эВ

Решение:
$\frac {\partial^2 {n}} {\partial {x}^2}+\frac {D_A_\bot} {D_A_|_|} \frac {\partial^2 {n}} {\partial {z}^2}=0$
$n(x=0,z)=n_0\cos(\frac {\pi z}{d})$
$n(x\to-\infty,z) -$ огр.
$n(x,z=\frac {d} {2})=0$
$n(x,z=-\frac {d} {2})=0$

Вопрос:
Правильно ли поставлены граничные условия?