Равномерное распределение

[integral2009]

Случайная величина $X$ равномерно распределена на отрезке $[-5,5]$. Найти $E\mathbf{X}$ и корреляционную матрицу случайного вектора $\mathbf{X}=\begin{pmatrix} X_1\\ X_2 \end{pmatrix}$

Где

a) $X_1=X^2$ и $X_2=X$

b) $X_1=X^3$ и $X_2=X$

-----------------------------
Понятно, что для равномерного распределения $X_2$ с $a=-5$ и $b=5$ матожидание $EX_2=\dfrac{b-a}{2}=0$

Дисперсия $DX_2=\dfrac{(b-a)^2}{12}=\dfrac{100}{12}=\dfrac{25}{3}$

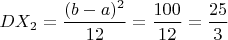
Но как найти $EX_1$ в a) Можно ли считать, что $X_1$ будет распределена равномерно?

Мне почему-то кажется, что нет.

Можно ли так считать? $f_X(x)=\dfrac{1}{b-a}=\dfrac{1}{10}$

a)

$EX_1=EX^2=\dfrac{1}{10}\displaystyle\int_{-5}^5x^2dx=...$

$DX_1=DX^2=\dfrac{1}{10}\displaystyle\int_{-5}^5x^4dx-EX^2=...$

$\operatorname{cov}(X_1,X_2)=EX^3-EX^2EX=...$

b)

$EX_1=EX^3=\dfrac{1}{10}\displaystyle\int_{-5}^5x^3dx=...$

$DX_1=DX^3=\dfrac{1}{10}\displaystyle\int_{-5}^5x^6dx-EX^3=...$

$\operatorname{cov}(X_1,X_2)=EX^4-EX^3EX=...$

Верно ли? Есть ли альтернативные методы решения данной задачи?

[profrotter]

integral2009 в сообщении #561324 писал(а):

a) Можно ли считать, что $X_1$ будет распределена равномерно?

Подробный ответ на этот вопрос найдётся в учебнике в разделе "Нелинейные преобразвания случайных величин" или "Законы распределения функций случайных величин" и тп.

По задаче в целом. Путь себе наметили в основных чертах правильный. Для надёжности неплохо бы посмотреть в учебнике материал "Математическое ожидание и дисперсия функции случайных величин", "Степенные моменты законов распределения" и тп.

[integral2009]

А что именно нужно проверить? Верна ли формула в Википедии для мат.ожидания функции случайной величины в непрерывном случае? А для Дисперсии?

$E\left[g(X)\right] = \displaystyle\int\limits_{-\infty}^{\infty}\!g(x) f_X(x)\, dx$

$D\left[g(X)\right] = \displaystyle\int\limits_{-\infty}^{\infty}\!g^2(x) f_X(x)\, dx-E^2\left[g(X)\right]$

Есть ли другие способы решения этой задачи?

Можно ли что-то сказать о законе распределения $X^2$ и $X^3$, если $X$ имеет равномерное распределение? Почему?

[--mS--]

integral2009 в сообщении #561448 писал(а):

Можно ли что-то сказать о законе распределения $X^2$ и $X^3$, если $X$ имеет равномерное распределение? Почему?

Можно. Его можно найти. А что - почему? Почему можно что-то сказать? Потому что это случайные величины, и у них есть распределения, значит, о них есть что сказать.
Это, разумеется, глупый метод для решения данной задачи, но уметь находить распределения функций от случайных величин полезно независимо ни от чего.

[integral2009]

--mS-- в сообщении #561475 писал(а):

integral2009 в сообщении #561448 писал(а):

Можно ли что-то сказать о законе распределения $X^2$ и $X^3$, если $X$ имеет равномерное распределение? Почему?

Можно. Его можно найти. А что - почему? Почему можно что-то сказать? Потому что это случайные величины, и у них есть распределения, значит, о них есть что сказать.
Это, разумеется, глупый метод для решения данной задачи, но уметь находить распределения функций от случайных величин полезно независимо ни от чего.

Ох, точно, есть же формула преобразования. Спасибо.

$f_Y(y) = f_X\left(g^{-1}(y)\right) \left\vert \dfrac{dg^{-1}}{dy}(y)\right\vert$

Но ведь $g^{-1}(y)$ может быть неоднозначно определена.

Ведь из того, что $X_1=X^2$ => $X=\pm\sqrt{X_1}$.

А какой знак выбирать - как узнать? Здесь ведь повезло, что равномерное распределение. Но так ведь будет не всегда...Если было бы показательное, к примеру?

-- Ср апр 18, 2012 16:46:51 --

Кажется понял - нужно и тот и другой знак рассматривать)

[--mS--]

А не проще по определению тупо найти функцию распределения?