Равномерная интегрируемость в ЗБЧ.

[mi.d]

Пусть $X_1,X_2,\ldots$ - н.о.р.с.в. с $E |X_1| < \infty$.
Обозначим $\xi_n = \frac1n \sum\limits_{i=1}^n X_i$.
Как известно, по УЗБЧ в форме Колмогорова, $\xi_n\to E X_1$ п.в.
А вот вопрос какой. Является ли последовательность $\xi_n$ равномерно интегрируемой?

Пока дошёл до того, что этот вопрос аналогичен сходимости $E |\xi_n| \to E |X_1|$.

[mi.d]

Ошибся.
Вопрос аналогичен сходимости $E |\xi_n| \to |E X_1|$.

[--mS--]

Это однозначно так. Например, в определении равномерной интегрируемости можно тупо заменить всюду модуль суммы суммой модулей, от этого все матожидания только увеличатся:

$$\sup_n\mathsf E\left\{\left|\tfrac{\sum_1^n X_i}{n}\right|\cdot I\left(\left|\tfrac{\sum_1^n X_i}{n}\right|\geqslant x\right)\right\} \leqslant \sup_n\mathsf E\left\{\tfrac{\sum_1^n |X_i|}{n}\cdot I\left(\tfrac{\sum_1^n |X_i|}{n}\geqslant x\right)\right\}\to 0 \ \textrm{при} \ x\to\infty .$$

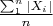
А равномерная интегрируемость последовательности $\frac{\sum_1^n |X_i|}{n}$ вытекает из её неотрицательности, плюс ЗБЧ для неё, плюс сходимость её матожиданий к предельному $\mathsf E\frac{\sum_1^n |X_i|}{n}\equiv \mathsf E|X_1|$.

[mi.d]

--mS--, снова Вы мне помогли :)
Спасибо, всё так и есть. Пытался пойти обходными путями, а следовало по определению.