Да. Будет. Отличие от заряда внутри сферы (если пренебречь ещё и дискретностью) в том, что воздействие единичного заряда
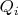
на сфере от расстояния пробного заряда P до точки сферы квадратично убывает, но количество этих зарядов на сфере в данном направлении квадратично возрастает. То есть если пространство внутри сферы разобьём на конусы (не обязательно круговые конусы) с вершиной в точке расположения заряда P, устремив телесный угол каждого к нулю (а их число, соответственно, к бесконечности) и каждому конусу сопоставим направленный в другую сторону с тем же телесным углом, то силы от зарядов на противоположно расположенных участках сферы взаимно компенсируются - если в одной стороне участок сферы дальше, то заряд его пропорционален квадрату расстояния от пробного заряда до участка, а сила от единичного заряда - обратно пропорциональна.
Для заряженного кольца это не выполняется, заряд в данном направлении пропорционален расстоянию до точки кольца, а не квадрату, так что по мере приближения пробного заряда к кольцу превалировать будут силы от ближайших точек.
Замена равномерно заряженного кольца системой дискретных зарядов даст дополнительную неравномерность распределения величины силы, она теперь будет зависеть не от одного расстояния от центра, но и от угла на ближайший заряд, и, кроме того, будет направлена не точно по радиусу кольца, её направление будет также зависеть от угла на ближайший заряд. Этот эффект тем менее выражен, чем больше зарядов, и при

исчезнет.