За время

зеркало отъедет на расстояние

. Длина пути луча увеличится на

. Если показатель преломления

, то изменение длины пути в точности равно изменению оптической разности хода. Если разность хода изменилась на целое число длин волн, сила тока осталась той же. Очевидно, что периоду изменения силы тока

соответствует изменение разность хода на

. Отсюда

. Фокус здесь в том, что

и

оп условию мало отличаются, поэтому изменение максимальной амплитуды, связанное с движением зеркала, практически одно и то же. Поэтому в качестве

можно взять их среднее арифметическое, или любую из них, с точностью до
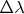
.

означает совпадение гребней через один. Тогда и

надо брать на как расстояние между двумя соседними максимумами.