Complex number

[man111]

Let $a,b,c$ be distinct Complex no. such that $\mid a\mid = \mid b \mid = \mid c\mid>0$

If $a+bc\;,b+ca\;,c+ab \in \mathbb{R}$. Then $abc=$

[Dave]

Пусть $|a|=|b|=|c|=r>0$. Тогда $a=re^{i\alpha}$, $b=re^{i\beta}$, $c=re^{i\gamma}$, где $\alpha, \beta, \gamma \in \mathbb R$.
Докажем вначале, что $r=1$. Предположим противное, $r \neq 1$. $z \in \mathbb R \Rightarrow \overline z \in \mathbb R$. Поэтому $\overline {a+bc} \in \mathbb R$ и $\overline {a+bc} (b+ca) \in \mathbb R$. Преобразовывая последнее выражение, получим: $\overline a b+ca\overline a+\overline c b\overline b+a\overline b c\overline c=\overline a b+cr^2+\overline c r^2+a\overline b r^2=\overline a b+a\overline b r^2+(c+\overline c)r^2$. 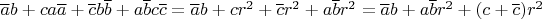Поскольку $c+\overline c \in \mathbb R$ и $r^2 \in \mathbb R$, то $x+\overline x r^2 \in \mathbb R$, где $x=\overline a b$. Если $\operatorname{Im} (x) = p$, то $\operatorname{Im} (x+\overline x r^2)=p-p r^2=p(1-r^2)$. Т.к. $r \neq 1$, то $p=0$ и $x \in \mathbb R$, т.е. $\overline a b \in \mathbb R$ и $a \overline b = \overline {\overline a b} \in \mathbb R$. Аналогичным образом получаем, что $\overline b c \in \mathbb R$. $b \neq 0$ и $c \neq 0$, значит $\frac {a \overline b} {\overline b c}=\frac a c=e^{i(\alpha-\gamma)} \in \mathbb R$. Такое возможно только в случае $\alpha-\gamma=2\pi n$, $n \in \mathbb Z$, т.е. $a=c$, что противоречит условию.
Итак, $r=1$. Докажем, что $\alpha+\beta+\gamma=2\pi n$, $n \in \mathbb Z$. Допустим противное. Тогда $0=\operatorname{Im} (a+bc)=\operatorname{Im} (e^{i\alpha}+e^{i(\beta+\gamma)})=\sin \alpha +\sin (\beta+\gamma)$. Такое возможно только когда $\beta+\gamma=-\alpha+2\pi n$, $n \in \mathbb Z$ или $\beta+\gamma=\alpha+(2k+1)\pi$, где $k \in \mathbb Z$. Первый вариант противоречит предположению, значит верен второй. Аналогично получаем, что $\gamma+\alpha=\beta+(2l+1)\pi$, $l \in \mathbb Z$ и $\alpha+\beta=\gamma+(2m+1)\pi$, $m \in \mathbb Z$. Складывая попарно эти равенства и деля на $2$, получим: $\alpha=(m+l+1)\pi$, $\beta=(k+m+1)\pi$, $\gamma=(k+l+1)\pi$. Но это означает, что минимум два из чисел $a$, $b$, $c$ равны, что противоречит условию.
Значит $\alpha+\beta+\gamma=2\pi n$, $n \in \mathbb Z$. Тогда $abc=e^{i(\alpha+\beta+\gamma)}=e^{2\pi n i}=1$.