Уважаемые участники форума! У меня не получается решить следующую задачу.
Пусть функция

, заданная на
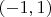
имеет

производных и при всех


. Надо доказать, что существует число

(не зависящее от

) такое, что при

уравнение

имеет на
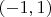
по крайней мере

разных решений.
Я могу решить при

. В этом случае достаточно выбрать

. А вот что потом... индукция?