Рассмотрим множество неотрицательных целых чисел и бинарные операции на нём: сложение, вычитание,
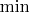
,
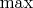
.
Будем, комбинируя эти операции, формировать новые. Например:

Константы запрещены.
Требуется сформировать операцию, которая была бы эквивалентна следующему выражению:

либо доказать, что это невозможно.