Нахождение периметра параллелограмма

[BENEDIKT]

Боковая сторона равнобедренного треугольника равна 5 м. Из точки, взятой на основании этого треугольника, проведены 2 прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

Обозначим равноб. треуг-к $ABC$ с основанием $AC$. Пусть D - точка на $AC$. Из т. $D$ проведены отрезки $DA_1$ к стороне $AB$ и $DC_1$ к стороне $BC$. Т. о. необходимо найти периметр параллелограмма $A_1DC_1B$.
Докажем, что треугольники $AA_1D $ и $DC_1C $- равнобедренные, тогда 2-х сумма соседних сторон параллелограмма будет равна боковой стороне тр-ка $ABC$.
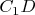
Сперва рассмотрим треуг-к $AA_1D $. Угол $A_1DC $- внешний по отношению к нему. По теореме он равен сумме не смежных с ним внутренних углов $A_1AD $ и $AA_1D$. Также он равен усмме углов $A_1DC_1$ и $C_1DC$, на которые его делит отрезок $C_1D$. Углы $AA_1D $ и $A_1DC_1$ - внутренние накрест лежащие при параллельных прямых $AB$ и $DC_1$ и секущей $A_1D$, т. е. эти углы равны. Тогда из равенства 2-х сумм выходит, что углы $A_1AD $ и $C_1DC $ равны(они также являются соответствующими).
На этом "затормозил", ибо не понимаю, как доказать равенство углов $A_1AD $ и $A_1DA $при основании тр-ка $AA_1D$.

[Human]

Рассмотрите соответственные углы при других двух параллельных прямых и стороне $AC$ и вспомните, наконец, про равнобедренность исходного треугольника.

[BENEDIKT]

Благодарю за помощь!