(Оффтоп)
grandmix писал(а):
вверх!
Нельзя так, по правилам.
Нет, конечно, не просто определение. Базисные векторы полностью определяются такими двумя требованиями.
Первое требование определяет направление векторов: они являются касательными к координатным линиям (которые получаются, если одну координату менять, а остальные зафиксировать). В случае цилиндрических координат это радиусы (меняется только

), окружности (меняется только

), ну, и вертикальные линии (меняется

).
Второе требование определяет длину векторов: при подходе, применяемом в Вашей книге, базисные векторы имеют единичную длину.
В более серьёзной теории это не всегда так, но здесь мы этому следуем.Конечно, чисто технически при расчете не обязательно надо прямо так непосредственно исходить из этих условий -- существуют удобные формулы. Вот как может выглядеть расчет.
Первый способ, "математический".
Находим вспомогательные векторы
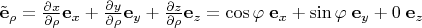
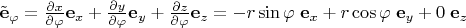
Они почти правильные, только не нормированы на единичную длину (в данном случае
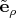
сразу получился хорошим, но
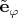
-- нет). Нормируем, получаем то, что в книге.
Кстати, с точки зрения "серьёзной теории" эти промежуточные неединичные векторы и есть правильные базисные векторы в цилиндрической системе, и нормировать их не надо -- но я Вам этого не говорил.Второй способ, "инженерный".
Имеется формула для разложения произвольного вектора

по ортонормированному базису, например,
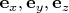
:
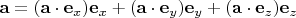
Применяем её к векторам
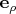
,
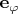
:
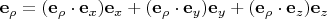
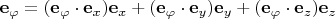
Так как все векторы в этой формуле единичные, скалярные произведения
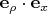
,

и т.д. равны просто косинусу угла между векторами. Остается как-то понять, исходя из конструкции цилиндрических координат, каковы же эти углы, и вместо скалярных произведений подставить их косинусы.